В урне находятся n плюс m одинаковых шаров, из которых n – белого, а m – черного цвета. Производятся подряд без возвращения n извлечений по два шара. Определить вероятность того, что каждый раз извлекались пары шаров разного цвета.

Будем использовать формулу гипергеометрической вероятности.

Рассмотрим первое извлечение:

Число способов извлечь 2 любых шара равна C²_n+m.

Благоприятный нам исход это шары разных цветов, то есть C¹_mC¹_n.

Тогда вероятность извлечь два первых шара разных цветов равна

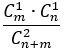
Далее, в урне становится на два шар...