Задана функция распределения случайной величины Х. Необходимо найти плотность вероятности, математическое ожидание и дисперсию данной случайной величины.
«Задана функция распределения случайной величины Х. Необходимо найти плотность вероятности, математическое ожидание и дисперсию данной случайной величины.»
- Теория вероятностей
Условие:
Задана функция распределения случайной величины Х:
Необходимо найти плотность вероятности, математическое ожидание и дисперсию данной случайной величины. Также требуется определить вероятность попадания в отрезок [0,25; 1].
Решение:
Плотность вероятности равна производной от функции распределения. Вычисляя производную, находим:
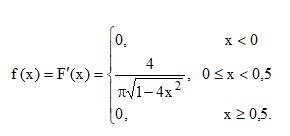
Математическое ожидание непрерывной случайной величины равно
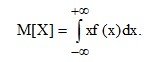
В поставленной задаче интегрируется кусочно-...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э